こんにちは、Frankです。
今日で28日目。もう一度高校数学を参考に高校数学を学習しています。
数学音痴の私ゆえ、骨格となる学習項目だけ準拠させて頂いています。
内容は噛み砕いて独自の表現法で書いています。
 ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄
・判別式 \(D>0, D=0, D<0\) をベースに2次関数の定数を求める
\(f(x)=ax^2+bx+c\hspace{1mm}(a>0)\) のグラフと \(x\) 軸 \(f(x)=0\) との関係
で、\(x\) 軸と交わる交点が2個の場合 \(D>0\)、\(x\) 軸と接する交点が1個
の場合 \(D=0\)、\(x\) 軸と交わらない交点が0個の場合 \(D<0\) となりま
すが、066ページに記された<2次方程式 \(ax^2+bx+c=0\) において
判別式を \(D\) とすると \(D=b^2-4ac\)>という表現から、112ページの
2次関数の例題は \(f(x)=x^2-ax+3\) と \(a\) で表現する代わりに判別
式に従って \(f(x)=x^2-bx+3\) と表現した方が判別式の計算でも間
違えないのではと思いました。
もちろん \(x\) の係数を出すのに \(b\) から始まるというのはおかしな話です
が、文系の私には判別式との整合性が気になるところでした。
判別式 \(D\) に応じたグラフを独自に作成してみました。
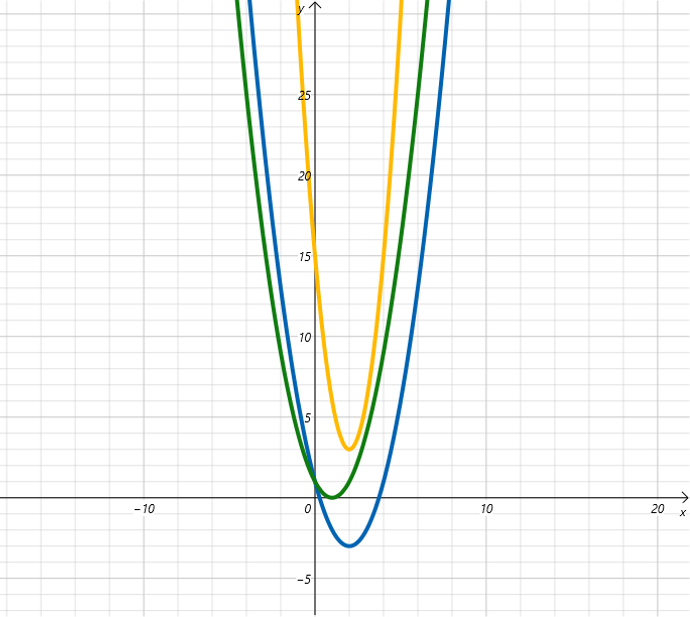
*青色のグラフは2次関数 \(y=x^2-4x+1\) で交点が2個あります。
頂点は \((2, -3)\) になります。
*緑色のグラフは2次関数 \(y=x^2-2x+1\) で交点は1個のみです。
頂点は \((1, 0)\) になります。
*黄色のグラフは2次関数 \(y=3x^2-12x+15\) で交点は0個です。
頂点は \((2, 3)\) になります。
因みに113ページの例題の右下点線内の説明が分かりにくかった方は、
「2次関数 \(-2x^2+ax-1<0\) より \(2x^2-ax+1>0\) となるの
で、2次不等式が \(>0\) となり \(y\) が常に \(0\) より上の値をとることから
\(x\) 軸と交わらない交点0個のグラフになるので \(D<0\) となる」と解
釈すればいいのではないでしょうか。
さすがに学習量が100ページを超えてくると、「私ならこう説明する」
という気持ちが湧いてきますが、千利休の「守破離」の思想を心に刻
み、最後の1ページを迎えるまで、心を無に読み進めていこうと思い
ます。
 |
![]()
次回はいよいよ<指数の法則>に入ります。お楽しみに b^^)
 ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄
【高校数学(数ⅠA・数ⅡB・数ⅢC)を復習する】でもっと学習する b^^)
【コンテント】当サイトで提供する情報はその正確性と最新性の確保に努めていま
すが完全さを保証するものではありません。当サイトの内容に関するいかなる間
違いについても一切の責任を負うものではありません。
【参考図書】『もう一度高校数学』(著者:高橋一雄氏)株式会社日本実業出版社
 ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄
私の姉妹ブログ実践英語の達人ではオンラインレッスンやクイズのご
案内をしています。良かったらご一読ください。
只今、人気ブログランキングに参加しています。
今日の[実践数学の達人]のランキングは——
