こんにちは、Frankです。
今日で122日目。今回は準公式をマスターして、簡単に面積を求める
方法を学習します。只、気を付けるべき点が何点かありそうです。
 ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄
・準公式 \(S = \int^\beta_{\alpha}a(x – \alpha)(x – \beta)dx = \frac{|a|}{6}(\beta – \alpha)^{3}\)
いつものように著作権の関係から、テキストもう一度高校数学の364、
365ページの例題の数式を若干変えて問題を解くことにします。
放物線 \(y = x^{2} + 3x + 2\) と直線 \(y = 2x + 8\) によって囲まれた部分
の面積 \(S\) を求めてみます。
\(y = x^{2} + 3x + 2 = (x + \frac{3}{2})^{2} – \frac{1}{4}\)
つぎに、曲線と直線との交点の \(x\) 座標を求めます。
\(x^{2} + 3x + 2 = 2x + 8\)
\(x^{2} + x – 6 = 0\)
\((x + 3)(x – 2) = 0\)
∴ \(x = -3、2\)
よって、下図のグラフより求める面積 \(S\) は
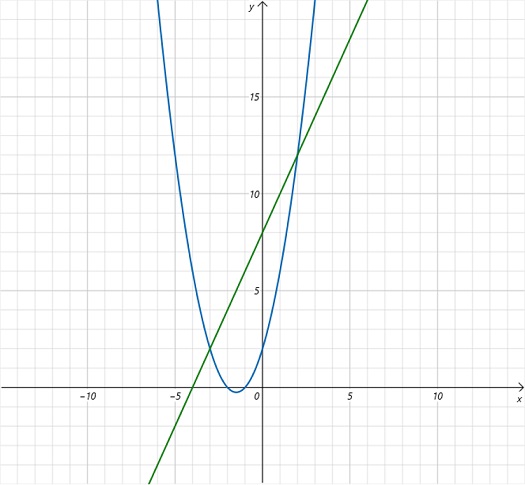
\(S = \int^2_{-3}(2x + 8 – x^{2} – 3x – 2)dx\)
\(= \int^2_{-3}(-x^{2} – x + 6)dx\)
\(= -\frac{1}{3}[x^{3}]^2_{-3} – \frac{1}{2}[x^{2}]^2_{-3} + 6[x]^2_{-3}\)
\(= -\frac{1}{3}(8 + 27) – \frac{1}{2}(4 – 9) + 6(2 + 3)\)
\(= \frac{-70 + 15 + 180}{6}\)
\(= \frac{125}{6}\)(答)
準公式を使うと、
\(a = 1、\alpha = -3、\beta = 2\)
\(S = \int^2_{-3}(x^{2} + x – 6)dx\)
\(= \frac{|1|}{6}\displaystyle\left\{(2 – (-3)\right\}^{3}\)
\(= \frac{1}{6}・5^{3}\)
\(= \frac{125}{6}\)(答)
検証できました。素晴らしい!d(^^)
次回は<ベクトル>に入ります。これは究めたいですね b^^)
 ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄
【高校数学(数ⅠA・数ⅡB・数ⅢC)を復習する】でもっと学習する b^^)
【コンテント】当サイトで提供する情報はその正確性と最新性の確保に努めていま
すが完全さを保証するものではありません。当サイトの内容に関するいかなる間
違いについても一切の責任を負うものではありません。
【参考図書】『もう一度高校数学』(著者:高橋一雄氏)株式会社日本実業出版社
 ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄
私の姉妹ブログ実践英語の達人ではオンラインレッスンや
クイズのご案内をしています。良かったらご一読ください。
只今、人気ブログランキングに参加しています。
今日の[実践数学の達人]のランキングは――
